해시-해시테이블-해싱
해시란?
- 데이터를 관리/유지하는 자료구조
- 리소스 < 속도
데이터를 관리 및 유지하는 자료구조로 리소스를 포기하고 속도를 취한 자료구조이다.

해시 자료구조를 이용해서 데이터를 정리해보자!
데이터를 해시 함수를 거쳐 테이블에 넣어야 한다. 어떻게 넣어야 나중에 보기가 편할까? 어떤 규칙이 있어야 할까?
똑같은 데이터가 올 때마다 똑같이 분류되어야 하는 규칙이 필요하다!
그 규칙성으로 정의된 것이 해시 함수이다.

데이터가 해시 테이블에 위와 같이 정리 되었을 때 해시 함수에는 어떤 규칙이 있었을까?
해시 함수는 /100 의 규칙을 가지고 있다.
123이라는 데이터가 왔을 때 나누기 100을 해서 1이라는 값이 나왔고, 그 값에 의해 해당 인덱스로 들어가게 된다.
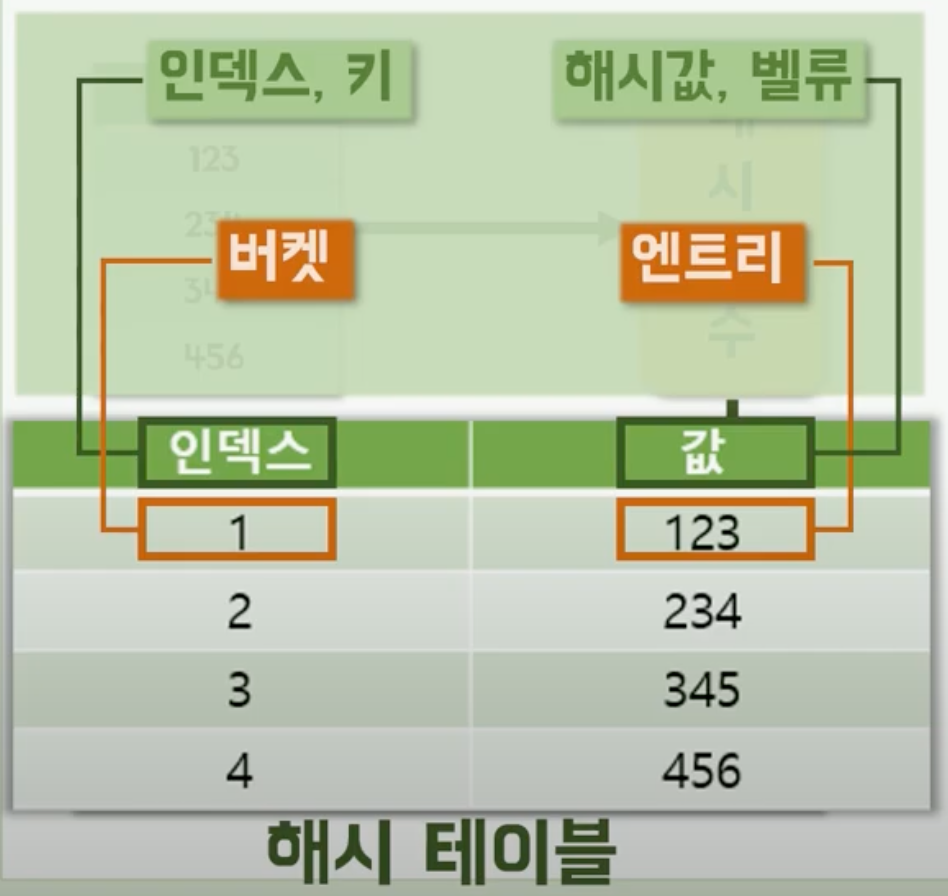
해시 테이블이란?
데이터가 해시 함수를 거쳐 분리된 이후, 정보가 저장되는 곳
- 인덱스, 키 ( 첫번째 컬럼 )
- 해시값, 벨류 ( 두번째 컬럼 )
인덱싱된 기준을 버켓이라고 하며, 버켓 안에 들어가 있는 값을 엔트리라고 한다.
해싱이란?
데이터들이 해시 함수에 의해 분류가 되고, 그 분류된 데이터는 해시 테이블 안에 규칙에 의해 들어간다.
이 모든 과정을 해싱이라고 한다.
해싱의 장점
데이터 접근의 빠른 속도! 자원을 이용하여 속도를 높인다.
예를 들어, 모든 데이터가 해시 테이블에 다 들어간 뒤에 345라는 숫자가 해시 테이블에 있는지 없는지 확인하고 싶다면?
345를 해시 함수에 의해서 변환시킨다. ▶︎ 3이라는 인덱스를 뽑아낸다. ▶︎ 3이라는 인덱스만 확인하면 된다. 하나하나 검사할 필요가 없다.
해시의 충돌
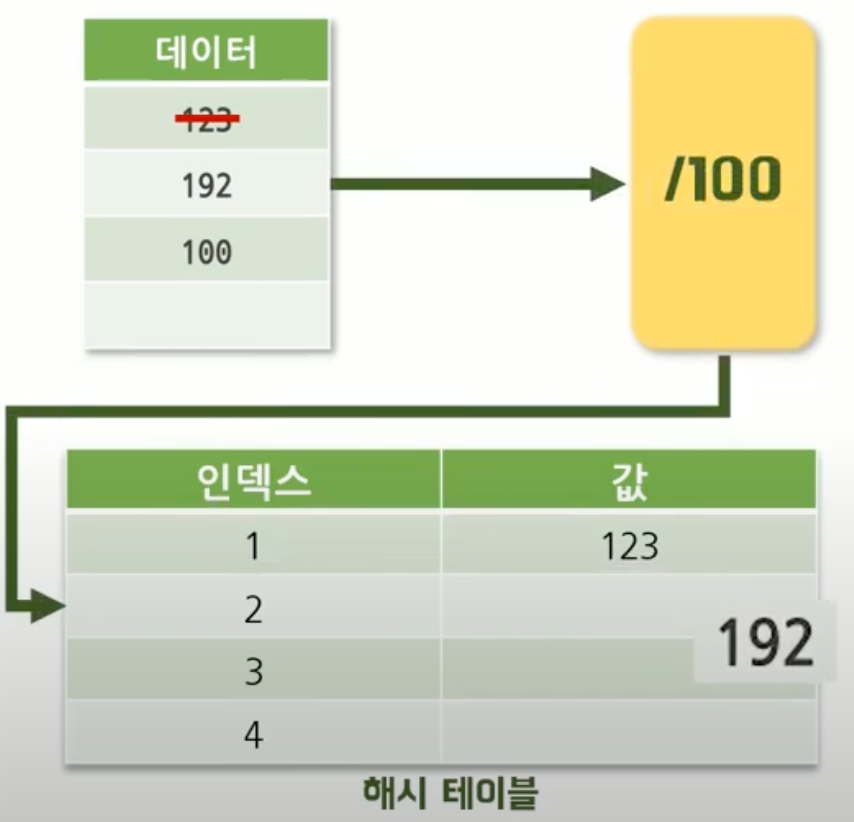
123이라는 데이터가 해시함수의 규칙에 의해 테이블로 들어간다.
이후 192라는 데이터가 해시 함수를 거쳐 테이블로 들어가려고 하니 자리가 없다...!
해시의 충돌을 해결하는 방법
1. 분리 연결법
1-1. 체이닝 (Chaining)
2. 개방 주소법 : 테이블 내 비어있는 공간의 새로운 인덱스를 찾자! 어떠한 방식으로 찾는 지에 따라 나뉨
2-1. 선형탐사 (Linear Probing)
2-2. 제곱 탐사법 (Quadratic Probing)
2-2. 이중해싱 (Double Hashing) : 해시 함수를 이중으로 사용
체이닝
해당 인덱스에 이미 값이 있으면, 그 뒤에 체인으로 연결 시키는 것이다.

안그래도 리소스를 많이 먹는데 계속 이어버리면 안돼! 리스트로 계속 값을 이어지게 해서 선형탐사 방법을 생각해낸다.
선형탐사
이미 만들어 놓은 버켓을 먼저 소모하자!

123, 315, 468이라는 데이터는 이미 들어갔고, 100이라는 데이터가 들어갈 차례
100은 해시 함수를 거쳐 1번 인덱스에 들어가야 하는데 이미 123이라는 값이 들어가 있다.
그럼 2번 인덱스에 밀어 넣는다. 값이 저장된 이후의 빈 공간을 탐색하여 다음 버켓 자리에 슥 밀어 넣는다.
이러한 선형 탐사법의 단점은 특정 해시 값의 주변에만 모두 채워져 있는 일차 군집화 문제에 취약하다.
같은 해시가 여러 번 나오는 상황이라면, 선형 탐사법을 사용하면 데이터가 연속되게 저장될 가능성이 높아진다.
또, 위에서 데이터가 더 들어온다면? 선형탐사할 자리도 없다!
그렇다면 테이블 리사이징이 필요하다.
제곱 탐사법
선형 탐사법의 일차 군집화 문제를 조금이나마 보완한 방법이다.
선형 탐사법과의 차이점은 탐사하는 폭이 고정폭이 아닌 제곱으로 늘어나는 부분이 차이가 있다.
첫 번째 충돌이 발생했을 때는 충돌 난 지점을부터 1의 제곱만큼, 두 번째 충돌이 발생했을 때는 2의 제곱만큼, 세 번째는 3의 제곱만큼 탐사하는 구간의 폭이 빠르게 커진다. 선형 탐사법 때와 동일한 상황에서 제곱 탐사법을 사용하면 해시 테이블은 아래와 같은 모양이 된다.

- 충돌이 발생하더라도 데이터의 밀집도가 선형 탐사법보다 많이 낮기 때문에 다른 해시값까지 영향을 받아서 연쇄적으로 충돌이 발생할 확률이 많이 줄어든다.
- 하지만 여전히 해시로 1이 여러 번 나오면 계속 충돌이 발생하고, 결국 데이터의 이차 군집화가(Secondary Clustering) 발생한다.
테이블 리사이징
테이블이 할당된 공간을 다 써서 더 이상 요소가 들어갈 자리가 없으면,
테이블의 크기를 늘려주고 기존의 데이터를 다시 해시 함수로 보내버린다. 그리고 테이블을 재정렬을 한다.
